矩阵连乘

矩阵连乘问题

1.题目描述

给定n个矩阵{A1,A2,...,An},其中Ai和A(i+1)是可乘的，i=1,2...n-1。考察这n个矩阵进行矩阵乘法运算时，通过括号改变运算的先后顺序，减少运算次数，找到最佳划分方法，求解最少运算次数。

补充信息

由于矩阵乘法满足结合律，矩阵的连乘可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定，也就是说该连乘积已完全加括号，则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。

2.解题思路

可使用动态规划算法解决此问题，它利用了子问题重叠的特点来减少重复计算。 首先定义一下几个数组： p[NUM]:存储各矩阵的行数和列数(两矩阵相乘，前一个矩阵的列数等于后一个矩阵的行数，因此只存储其中的一个) dp[i][j]:表示从第 i 个矩阵到第 j 个矩阵的最小乘法次数。 s[i][j]:储从矩阵i乘到矩阵j的最外层断点 定义符号: m [ i , j ]表示的A[i]乘到A[j]最少乘次,m[ i , j ]即问题的最优解 递归公式如下：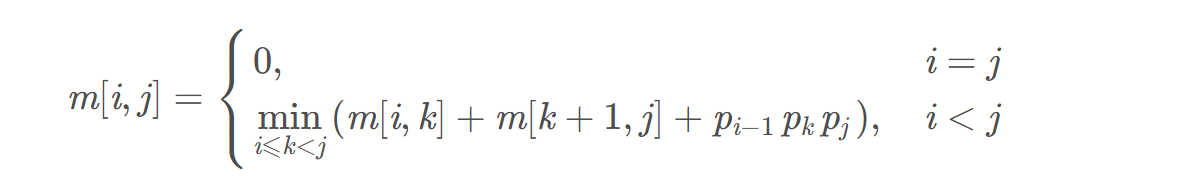

输入格式

第一行输入一个数n，代表矩阵的个数

第二行输入 n+1 个数，代表这n个数组的行数和列数

输出格式

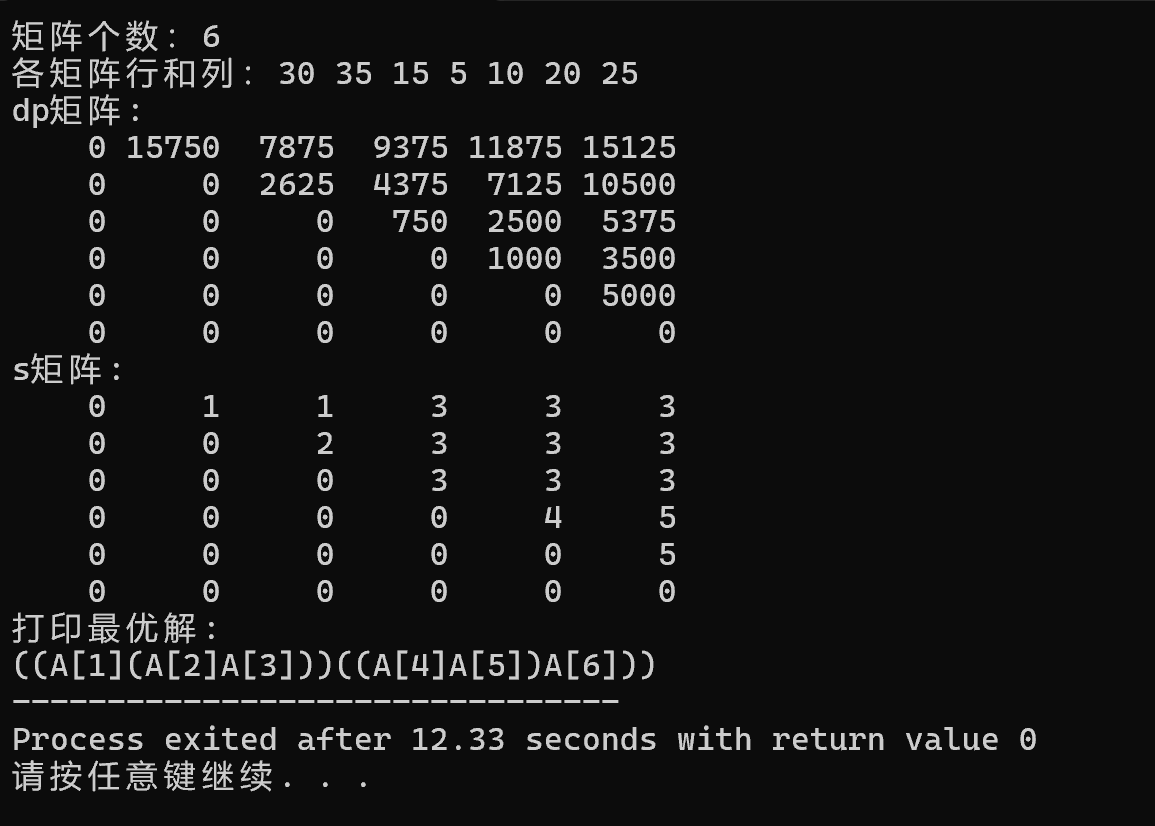
打印二维数组dp，个元素宽度为5，右对齐

打印二维数组s，格式相同

打印已完全加括号的最优解

测试用例

1

3.代码实现

//矩阵连乘问题
#include<iostream>
#include<vector>
#include<iomanip>
using namespace std;
const int NUM = 99;
int p[NUM] = {0};		//存储各矩阵的行数和列数
int dp[NUM][NUM] = {0};		//表示从矩阵i乘到矩阵j的最少次数
int s[NUM][NUM] = {0};		//存储从矩阵i乘到矩阵j的最外层断点
int MatrixChain(int i, int j){		//用递归的方法计算dp矩阵和s矩阵
	if(i == j){
		return 0;
	}
	int min = 999999999;
    for(int k = i; k < j; k++){
		if(MatrixChain(i,k) + MatrixChain(k + 1,j) + p[i-1] * p[k] * p[j] < min){
			min = MatrixChain(i,k) + MatrixChain(k + 1,j) + p[i-1] * p[k] * p[j];
			s[i][j] = k;
		}
	}
	dp[i][j] = min;
	return min;
}
void OutPut(int i,int j){		//打印最优解
	if(i == j){
		cout << "A[" << i << "]";
		return;
	}
	cout << "(";
	OutPut(i,s[i][j]);
	OutPut(s[i][j] + 1,j);
	cout << ")";
}
int main(){
	int n;
	cout << "矩阵个数：";cin >> n;
	cout << "各矩阵行和列：";
	for(int i = 0; i <= n; i++){
		cin >> p[i];
	}	
	cout << "dp矩阵:"<< endl;
	int x = MatrixChain(1,n);
	for(int i = 1;i <= n;i++){
		for(int j = 1;j <= n;j++){
			cout << setw(5) << right << dp[i][j] << " ";
		}
		cout << endl;
	}
	cout << "s矩阵:" << endl;
	for(int i = 1;i <= n;i++){
			for(int j = 1;j <= n;j++){
				cout << setw(5) << right << s[i][j] << " ";
			}
			cout << endl;
		}
	cout << "打印最优解:" << endl;
	OutPut(1,n);
	return 0;
}