递归与分治

1. 递归 直接或间接地调用自身的算法称为递归算法，用函数自身给出定义的函数称为递归函数

picture 0

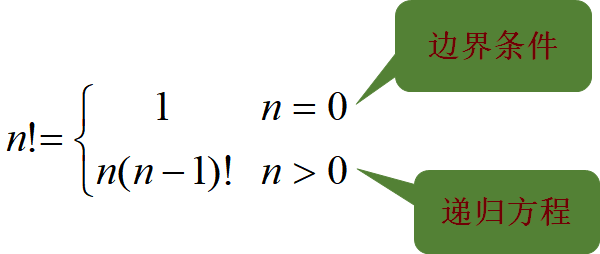
2. 分治

（1）思想 分治法的设计思想是，将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

凡治众如治寡，分数是也。
						----孙子兵法

（2）具体做法 将要求解的较大规模的问题分割成k个更小规模的子问题。 对这k个子问题分别求解。如果子问题的规模仍然不够小，则再划分为k个子问题，如此递归的进行下去，直到问题规模足够小，很容易求出其解为止。

divide-and-conquer(P)
  {
    if ( | P | <= n0) adhoc(P);   //解决小规模的问题
    divide P into smaller subinstances P1,P2,...,Pk；//分解问题
    for (i=1,i<=k,i++)
      yi=divide-and-conquer(Pi);  //递归的解各子问题
    return merge(y1,...,yk);  //将各子问题的解合并为原问题的解
  }

分析： 一个分治法将规模为n的问题分成k个规模为n／m的子问题去解。设分解阀值n0=1，且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间，则有：

picture 1

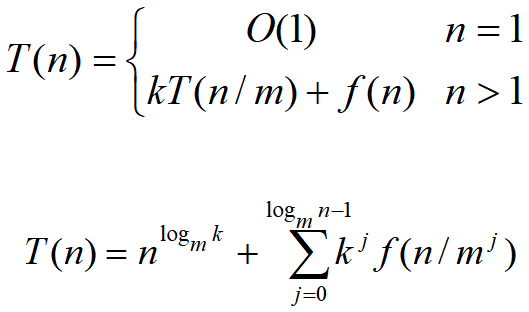
复杂性方程求解：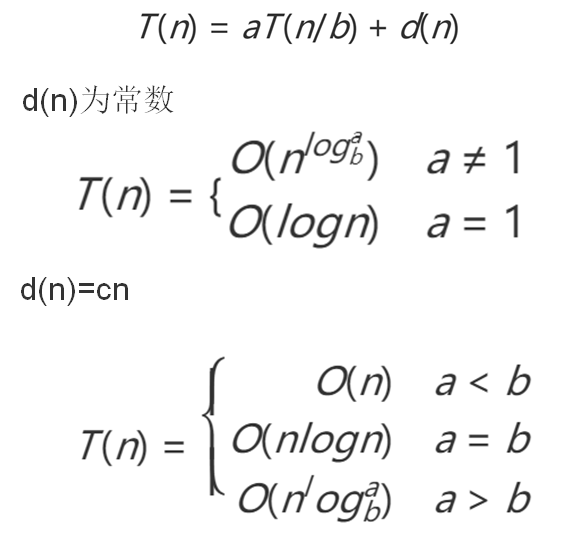

（3）适用条件 1、该问题的规模缩小到一定的程度就可以容易地解决； 2、该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质 3、利用该问题分解出的子问题的解可以合并为该问题的解； 4、该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。