寻找两个有序数组的中位数
寻找两个有序数组的中位数
1. 题目描述
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2 。
请你找出这两个有序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
示例 1:
nums1=[1,3]
nums2=[2]
则中位数是2.0
示例 2:
nums1=[1,2]
nums2=[3,4]
则中位数是(2+3)/2=2.5
2. 解法
2.1.1解法一(不限制时间复杂度)
将两个数组使用归并的思想,进行整合,然后求解。
这种解法的时间复杂度是O(m + n)。
2.1.2代码实现
public static double Test4S2(int[] nums1, int[] nums2) {
List<Integer> array = new ArrayList<>(10);
int size1 = nums1.length;
int size2 = nums2.length;
int index1 = 0;
int index2 = 0;
while(index1 != size1 || index2 != size2){
if(index1 == size1){
for (int i = index2; i < size2; i++){
array.add(nums2[i]);
}
break;
}else if (index2 == size2){
for (int i = index1; i < size1; i++){
array.add(nums1[i]);
}
break;
}
array.add(nums1[index1] < nums2[index2] ? nums1[index1] : nums2[index2]);
if(nums1[index1] < nums2[index2]){
if(index1 < size1)
index1++;
}
else{
if(index2 < size2) index2++;
}
}
int sizeArray = array.size() / 2;
if(array.size() % 2 == 0) return (array.get(sizeArray - 1) + array.get(sizeArray)) / 2.00;
else return array.get(sizeArray);
}
2.2.1 解法二
时间复杂度的限制O(log(m+n)),可以用二分查找法来解决。
中位数的概念其实可以理解为,将数组整体分为两个部分,一边大于等于中位数,一边小于等于中位数。那么在这道题目中两个有序数组,我们可以将两个数组并排画一条线,这条线能正好划分左右两个部分,而我们的任务就是要找到这条线。
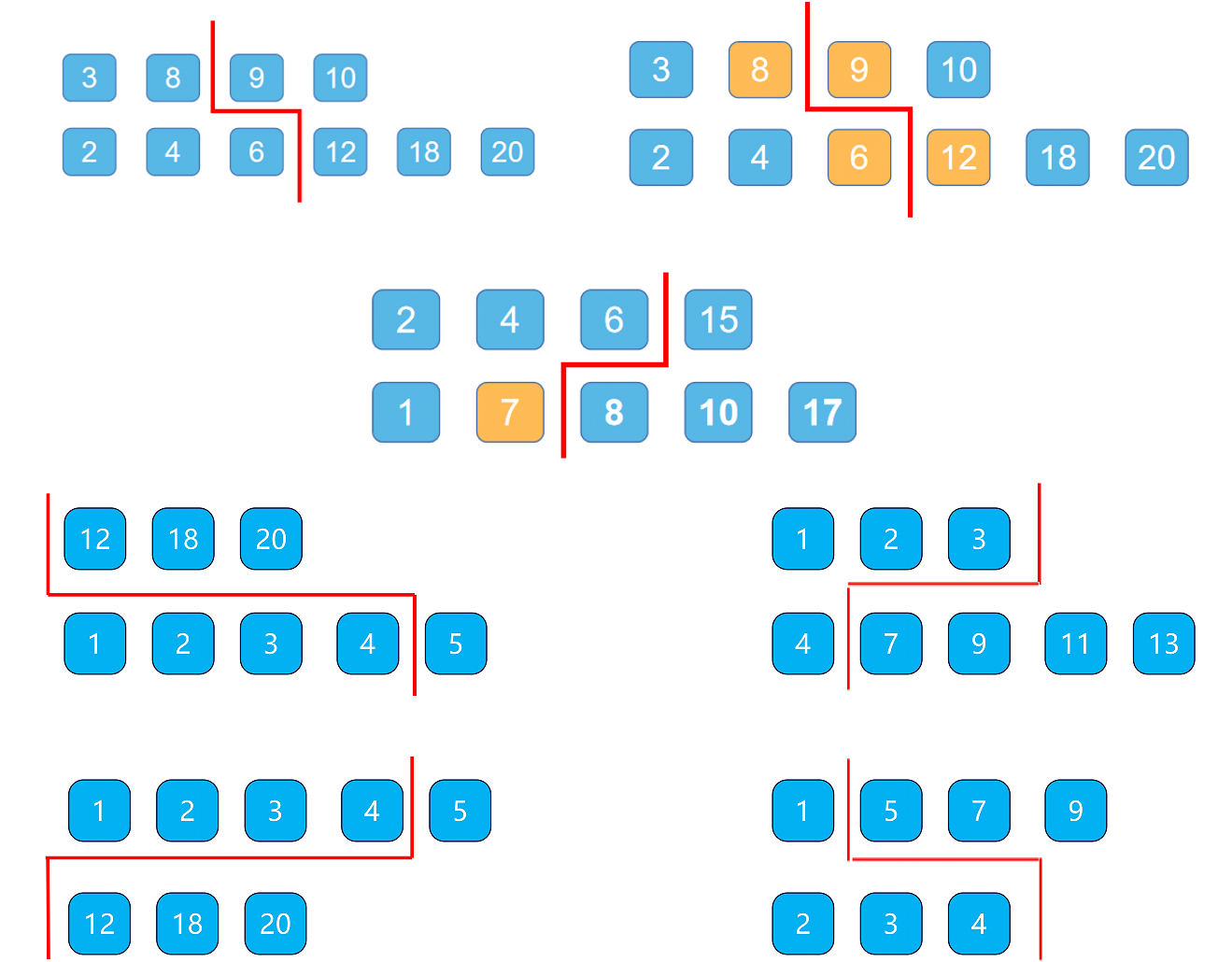
就是为了找到i,j连起来的线,能够正好将两个数组划分成左右两个部分,划分好了之后,只需要记录左边最大的值和右边最小的值,通过这两个值求解中位数就可以了,研究之后你就会发现i和j的关系是
i + j = m - i + n - j
因为左边部分和右边部分的数量要相等,有了这个之后,我们只要最开始随机确定i(直接在小数组中间取i),然后通过左右移动i(j移动的方向和i相反)找到我们要的那条线。不过一定要小心边界问题,对于边界要进行处理好。
2.2.2 代码实现
public static double Test4S3(int[] nums1, int[] nums2) {
int m = nums1.length;
int n = nums2.length;
if (m > n) {
return Test4S3(nums2,nums1); // 保证 m <= n
}
int iMin = 0, iMax = m;
while (iMin <= iMax) {
int i = (iMin + iMax) / 2;
int j = (m + n + 1) / 2 - i;
if (j != 0 && i != m && nums2[j-1] > nums1[i]){ // i 需要增大
iMin = i + 1;
}
else if (i != 0 && j != n && nums1[i-1] > nums2[j]) { // i 需要减小
iMax = i - 1;
}
else { // 达到要求,并且将边界条件列出来单独考虑
int maxLeft = 0;
if (i == 0) { maxLeft = nums2[j-1]; }
else if (j == 0) { maxLeft = nums1[i-1]; }
else { maxLeft = Math.max(nums1[i-1], nums2[j-1]); }
if ( (m + n) % 2 == 1 ) { return maxLeft; } // 奇数的话不需要考虑右半部分
int minRight = 0;
if (i == m) { minRight = nums2[j]; }
else if (j == n) { minRight = nums1[i]; }
else { minRight = Math.min(nums2[j], nums1[i]); }
return (maxLeft + minRight) / 2.0; //如果是偶数的话返回结果
}
}
return 0.0;
}
2.3.1 解法三
使用递归二分法进行解决
中位数其实就是第 (总长度)/2 小的数(奇偶我就不多说了,为了方便我就直接用奇数了),以为两个数组都是有序的,所以我们每次通过循环排除K的一半,直到最后找到K。
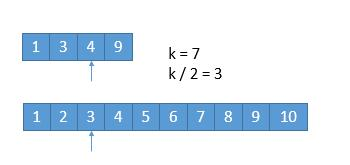
这个时候K/2等于3,然后我们比较两个数组的第三个位置上的数,就可以排除小的那一边的三个数一定不是第K小,然后我们这个时候将排除的数标记。
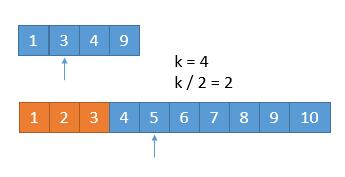
这个时候因为我们已经排除了3个数,接下来我们只要在新的两个数组中,找到K-3也就是第4小的数就可以了,同样的,将K比较K一半为止的数,重复如此。
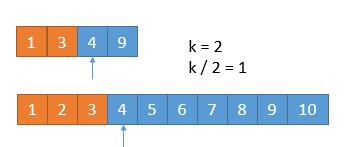
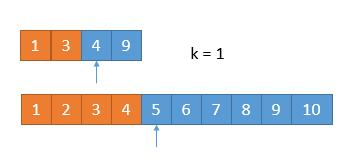
所以我们采用递归的思路,为了防止数组长度小于 k/2,所以每次比较 min(k/2,len(数组)对应的数字,把小的那个对应的数组的数字排除,将两个新数组进入递归,并且 k 要减去排除的数字的个数。递归出口就是当 k=1 或者其中一个数字长度是 0 了。
private static int kMinNum(int start1, int end1, int[] nums1, int start2, int end2, int[] nums2, int k){
int len1 = end1 - start1 + 1;
int len2 = end2 - start2 + 1;
if(len1 > len2) return kMinNum(start2, end2, nums2, start1, end1, nums1, k);
if(len1 == 0) return nums2[start2 + k - 1];
if(k == 1) return Math.min(nums1[start1], nums2[start2]);
int i = start1 + Math.min(len1, k / 2) - 1;
int j = start2 + Math.min(len2, k / 2) - 1;
if(nums1[i] > nums2[j]){
return kMinNum(start1, end1, nums1, j + 1, end2, nums2,k - (j - start2 + 1));
}else{
return kMinNum(i + 1, end1, nums1, start2, end2, nums2, k - (i - start1 + 1));
}
}
public static double Test4S1(int[] nums1, int[] nums2) {
int n = nums1.length;
int m = nums2.length;
int left = (n + m + 1) / 2;
int right = (n + m + 2) / 2;
return (kMinNum(0, n - 1, nums1, 0, m - 1, nums2, left) + kMinNum(0, n - 1, nums1, 0, m - 1, nums2, right)) * 0.5;
}
