木材加工

题目背景

要保护环境

题目描述

木材厂有 $n$ 根原木，现在想把这些木头切割成 $k$ 段长度均为 $l$ 的小段木头（木头有可能有剩余）。

当然，我们希望得到的小段木头越长越好，请求出 $l$ 的最大值。

木头长度的单位是 $\text{cm}$，原木的长度都是正整数，我们要求切割得到的小段木头的长度也是正整数。

例如有两根原木长度分别为 $11$ 和 $21$，要求切割成等长的 $6$ 段，很明显能切割出来的小段木头长度最长为 $5$。

输入格式

第一行是两个正整数 $n,k$，分别表示原木的数量，需要得到的小段的数量。

接下来 $n$ 行，每行一个正整数 $L_i$，表示一根原木的长度。

输出格式

仅一行，即 $l$ 的最大值。

如果连 $\text{1cm}$ 长的小段都切不出来，输出 0。

样例 #1

样例输入 #1

3 7
232
124
456

样例输出 #1

114

提示

数据规模与约定

对于 $100\%$ 的数据，有 $1\le n\le 10^5$，$1\le k\le 10^8$，$1\le L_i\le 10^8(i\in[1,n])$。

题解

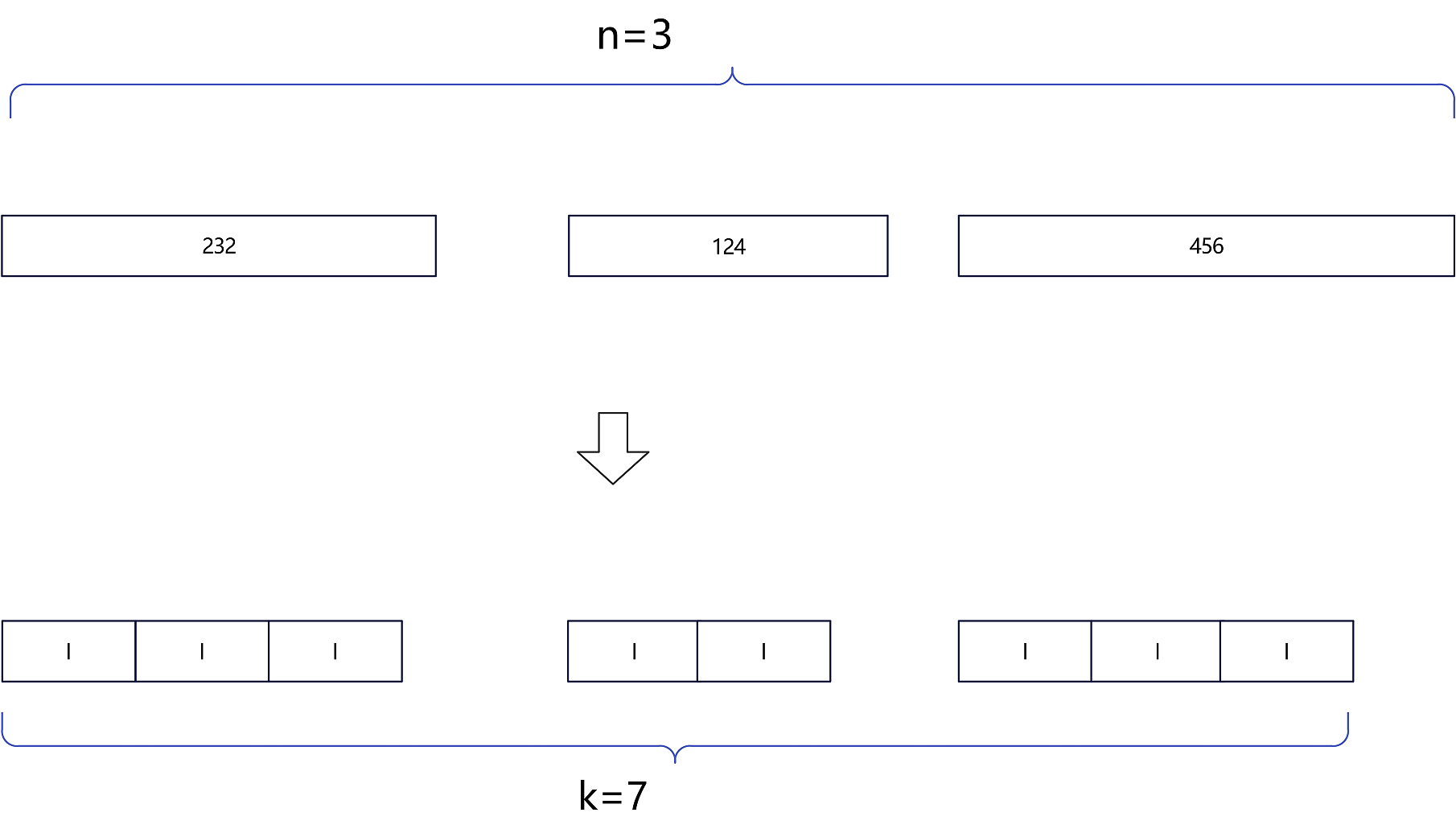
以样例分析，n = 3,即三根木头；k = 7,即截成 7小段木头，求小段木头可截的最大长度x,给出三段木头的长度：232,124,456 。

为了和左边界 l 区分，我们把题目中木段长度 l 统一换为 x

用暴力思想：x = 1cm，一：232//1 = 232；二：124//1 = 124；三：456//1 = 456 则k = 232 + 124 + 456 = 812 即 x = 1,k = 812, 同理得： x = 2, k = 406, x = 3, k = 270, ...... x = 80, k = 8,x = 81, k = 8, ...... x = 95, k = 7, x = 96, k = 7, ...... x = 115,k =6, x = 116,k = 6, ...... 由此发现答案具有单调性，且 k = 7时 x 是一段区间,我们找到第一个k = 6的x然后x - 1即是k = 7时每段最大的长度

用二分答案：由题意知， k 不为零时x最大为456，则正确答案一定就在 1—456 这个区间里。 即 l = 1,r = 456 ，mid = (l+r)//2

picture 0

我们定义一个让你的代码简洁明了的check函数，x = mid,根据x和k的单调性，就是咱们用sum += a[i]//x,sum就是咱们求出的段数，和 题目已知段数k做对比，如果 sum = k，返回 Ture，说明咱们目前的x小于正确答案，正确答案大于 x，然后用ans记录当前mid,以防这个mid是正确答案（记录最佳答案）跳出循环后 ans就是最佳答案。然后应该把 左边界l = mid+1,以缩短 x的范围。

如果sum < k,则说明mid大于正确答案,正确答案小于mid，所以应该把右边界r = mid - 1。

n, k = map(int, input().split())
a = []
for i in range(0, n):
    x = int(input())
    a.append(x)
a.sort()


def check(x):
    sum = 0
    for i in range(0, n):
        sum += a[i] // x
    if sum >= k:
        return True
    else:
        return False


l = 1
r = a[n - 1]
ans = 0
while l <= r:
    # 欧耶耶，l = r，mid = l = r,存在 mid，如果没有=，则mid不存在？
    mid = (l + r) // 2
    if check(mid):
        l = mid + 1
        ans = mid
    else:
        r = mid - 1
print(ans)