棋盘覆盖问题

题目描述

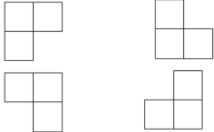
在一个 2^k*2k 个方格组成的棋盘中，若恰有一个方格与其他方格不同，则称该方格为特殊方格，且称该棋盘为一特殊棋盘。用4种不同的L型骨牌覆盖一个给定的特殊棋盘（即特殊方格的位置已经确定了）上除去特殊方格外的所有方格，并且任何两个L型骨牌不得重复覆盖。

图 0

输入格式：

• 第一行输入一个整数N，代表棋盘规模(N为2的k次幂)
• 第二行输入两个整数x、y，代表特殊方格的行号、列号。其中，x、y均从0开始

输出格式：

• 一个二维数组，以矩阵的形式输出，表示棋盘的覆盖情况。

输入样例：

棋盘规模： 8 行号、列号： 3 4

输出样例：

3   3   4   4   8   8   9    9 3   2   2   4   8   7   7    9 6   2   5   5  11  11 7   10 6   6   5   1  -1   11 10 10 18 18 19 1   1   13 14 14 18 17 19 19 13 13 12 14 21 17 17 20 16 12 12 15 21 21 20 20 16 16 15 15

解题思路

当 K > 0 时，可以将 2^k*2k的棋盘划分为4个 2^(k-1)*2(k-1)的子棋盘。这样划分后，由于原棋盘只有一个特殊方格，所以这4个子棋盘中只有1个子棋盘中有特殊方格，其余3个子棋盘中没有特殊方格。为了将这3个没有特殊方格的子棋盘转化为特殊棋盘，以便采用递归方法求解，可以用一个L型骨牌覆盖这3个较小的棋盘的会合处，从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种划分策略，直至将棋盘分割为 1*1 的子棋盘。

代码实现

#include<iostream>
#include<vector>
using namespace std;
vector <vector <int>> A(100,vector<int>(100,0));
int t = 0;
void chessBoard(int tr,int tc,int dr,int dc,int size){
	if(size == 1) return ;
	int s = size / 2;
	int x = ++t;		//在每一层递归调用上都为同一个值，且一定会在三个象限上各出现一次，递归每深入一层x+1
	//第一象限
	if((dr < tr + s)&&(dc < tc + s)){//如果特殊方格位于该区域,则在该区域内递归调用该函数
		chessBoard(tr,tc,dr,dc,s);
	}else{
		//否则覆盖该区域的右下角方格（此方格在递归的意义上也成为特殊方格）
		A[tr + s - 1][tc + s -1] = x;
		chessBoard(tr,tc,tr + s - 1,tc + s - 1,s);
	}
	//第二象限
	if((dr < tr + s)&&(dc >= tc + s)){
		chessBoard(tr,tc + s,dr,dc,s);
	}else{
		A[tr + s - 1][tc + s] = x;
		chessBoard(tr,tc + s,tr + s - 1,tc + s,s);
	}
	//第三象限
	if((dr >= tr + s)&&(dc >= tc + s)){
			chessBoard(tr + s,tc + s,dr,dc,s);
	}else{
		A[tr + s][tc + s] = x;
		chessBoard(tr + s,tc + s,tr + s,tc + s - 1,s);
	}
	//第四象限
	if((dr >= tr + s)&&(dc < tc + s)){
			chessBoard(tr + s,tc,dr,dc,s);
	}else{
			A[tr + s][tc + s - 1] = x;
			chessBoard(tr + s,tc,tr + s,tc + s - 1,s);
	}
	return;
}
int main(){
	int n;
	cout<<"棋盘规模："<<endl;
	cin >> n;
	if (((n & (n-1)) != 0)||(n == 0)){
		cout << "非法值"<<endl;
		exit(-1);
	}
	int i,j;
	cout<<"行号、列号："<<endl;
	cin >> i >> j;
	if((i > n)||(j > n)){
			cout << "非法值"<<endl;
				exit(-1);
	}
	A[i][j] = -1;
	cout<<"----------------------------------"<<endl;
	chessBoard(0,0,i,j,n);
	for(int i = 0;i < n;i++){
	        for(int j = 0;j < n;j++){
				cout << A[i][j]<<" "; 
			}		
			cout << endl;
		}
	return 0;
}