Python 逻辑回归
Python 逻辑回归
1. 什么是逻辑回归?
线性回归,线性回归是用来处理和预测连续标签的算法。今天学的逻辑回归,是一种名为“回归”的线性分类器,本质其实由线性回归变化而来。
线性回归回顾: 其中:是截距项,是系数。 写成矩阵的形式:
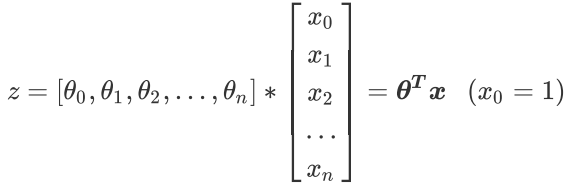
2. 逻辑回归模型
现在需要一种分类算法,意味着我需要输出的函数值是0或者1。那说明我们的标签是离散型变量,尤其是,如果是满足0-1分布(该事件发生的概率为p,不发生的概率为1-p)的离散型变量,我们要怎么办呢? 我们可以通过引入联系函数(link function),将线性回归方程z变换为g(z),并且令g(z)的值分布在(0,1)之间,且当g(z)接近0时样本的标签为类别0,当g(z)接近1时样本的标签为类别1,这样就得到了一个分类模型。而这个联系函数对于逻辑回归来说,就是Sigmoid函数:

注意: Sigmoid函数是一个S型的函数,当自变量z趋近正无穷时,因变量g(z)趋近于1,而当z趋近负无穷时,g(z)趋近于0,它能够将任何实数映射到(0,1)区间,使其可用于将任意值函数转换为更适合二分类函数。
线性回归中,将z带入,可以得到二元逻辑回归模型的一般形式:
3. 损失函数
逻辑回归的损失函数由极大似然估计法得出,对于某一个样本 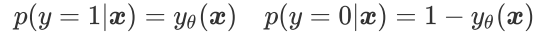
对于mw个样本: 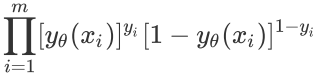
负对数: 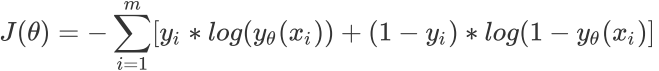
其中,表示求解出来的一组参数,m是样本的个数,是样本i上真实的标签,是样本i上,基于参数计算机来的逻辑回归的返回值,是样本i各个特征的取值。目标是求解出便最小的取值。 在损失函数中, x,y 都是已知量, 是未知量。 接下来,我只用找最小值时的参数。
4. 梯度下降求解参数过程
以最著名也最常用的梯度下降法为例,来看看逻辑回归的参数求解过程究竟实在做什么。现在,我们寻求的是损失函数的最小值,也就是图像的最低点。 图像为,其中假设我们输入为两个特征 ,那么我们仅有两个参数 ,假设模型没有截距项 。 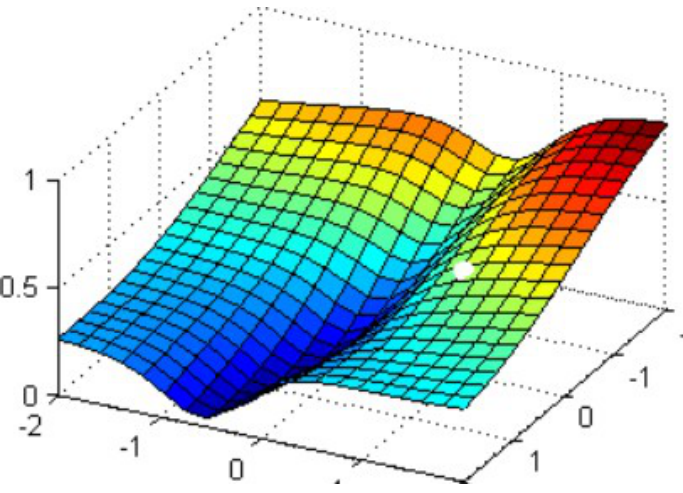
在这个图像上随机放一个小球,当我松手,这个小球就会顺着这个华丽的平面滚落,直到滚到 深蓝色的区域——损失函数的最低点。梯度下降,其实就在众多中遍历,小球每走一步,就得到一组。
- 小球滚动的方向:梯度 梯度:在多元函数上对各个自变量求偏导数,再把这个偏导数用向量的方式写出来,就是梯度。梯度的方向是函数值变化最快的方向。我们就需要沿着这个方向去让小球下降。 对于的梯度(n个参数):,梯度向量为
损失函数: 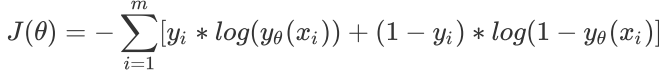
损失函数的梯度(梯度方向为函数值上升最快的方向) 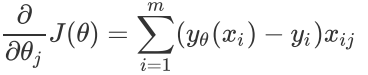
遍历过程: 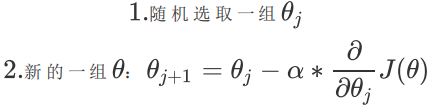
规定小球下降的速度:步长 步长不是一个真正的物理距离,是梯度向量的大小上的一个比例。我们在学习过程中,如何选取合适的步长,非常关键。
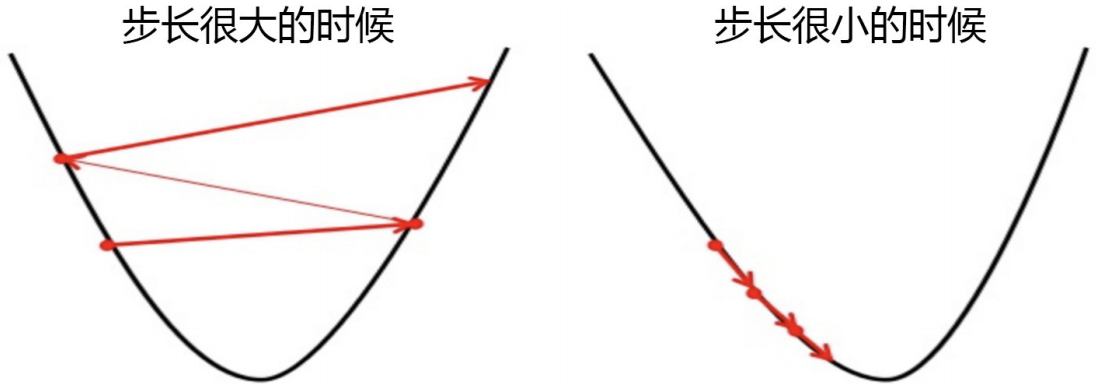
picture 9
5. SKlearn中的逻辑回归
class sklearn.linear_model.LogisticRegression (penalty='I2', dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_acaling=1, class_weight=None, random_state=None, solver=’warn’, max_iter=100, multi_class=’warn’, verbose=0, warm_start=False, n_jobs=None)
重要参数:
- 正则化项:penalty='l2'
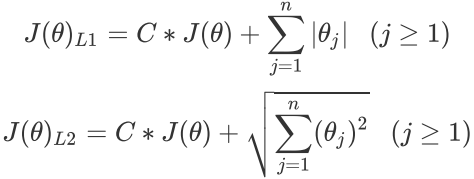
L1:会将参数压缩为0 L2:只会让参数尽量小,不会为0 正则化:帮助我们提高模型的泛化能力,减少过拟合现象。L1正则化和L2正则化是两种常用的正则化方法,它们各有特点,适用于不同类型的问题。L1正则化的主要作用是引导模型更加关注那些绝对值较大的权重,从而在一定程度上防止过拟合。在机器学习领域,L1正则化通常用于稀疏模型,即那些大部分权重为零的模型,如Lasso回归等。 L2正则化是指权值向量w中各个元素的平方和然后再求平方根。L2正则化的主要作用是减少模型的复杂性,从而在一定程度上防止过拟合。在机器学习领域,L2正则化通常用于Ridge回归等模型。
正则化的基本原理是通过惩罚模型的复杂度或参数的大小,以防止模型在训练数据中过度适应噪声或不相关的特征。正则化使模型倾向于选择更简单的参数设置或稀疏的特征,从而提高模型的泛化能力和对未见数据的预测准确性。
C正则化强度的倒数:C=1.0 必须是一个大于0的浮点数,不填写默认1.0,即默认正则项与损失函数的 比值是1:1。 C越小,损失函数会越小,模型对损失函数的惩罚越重,正则化的效力越强,参数会逐渐被压缩得越来越小。
.梯度下降的最大迭代次数(代替步长):max_iter=100 在我们开始梯度下降之前,我们并不知道什么样的步长才合适,但梯度下降一定要在某个时候停止才可以,否则模型可能会无限地迭代下去。因此,在sklearn当中,我们设置参数max_iter最大迭代次数来代替步长,帮助我们控制模型的迭代速度并适时地让模型停下。max_iter越大,代表步长越小,模型迭代时间越长,反之,则代表步长设置很大,模型迭代时间很短。
- 参数列表




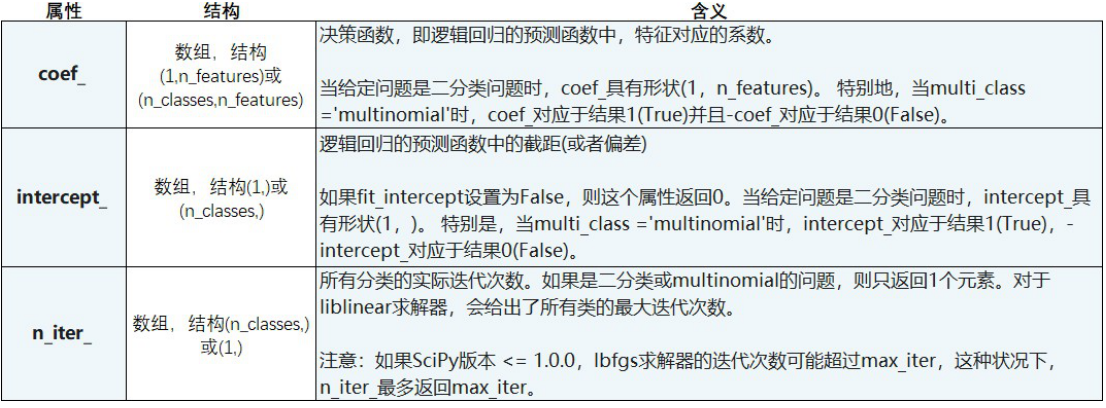
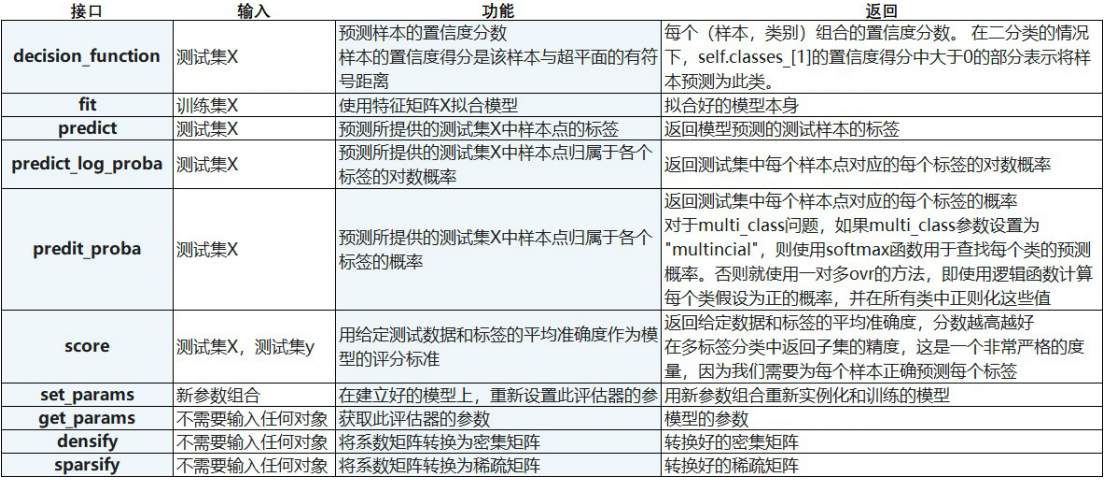
6.模型评估
6.1 错误率与精度
错误率:分错的样本占样本总数的比例 精度:1-E
6.2 误差
误差:真实值与预测值的差异 训练误差:训练集上的误差/经验误差 泛化误差:新样本上的误差
6.3 查全率、查准率 F1
查准率Precision:关注的问题是筛选的样本中是正样本的比例=查正确的样本/预测结果是这个类型的总样本数。 召回率 查全率Recall:关注的问题是筛选的样本中有多少比例的正样本被筛选出来=查正确的样本/真正是这个类型的总样本数。
6.4 F1
F1 Score:对于查准率和查全率的调和平均,F1-score 越大越好。
- 逻辑回归对线性关系的拟合效果好到丧心病狂,特征与标签之间的线性关系极强的数据,比如金融领域中的信用卡欺诈,评分卡制作,电商中的营销预测等等相关的数据,都是逻辑回归的强项。逻辑回归在金融领域,尤其是银行业中的统治地位依然不可动摇(相对的,逻辑回归在非线性数据的效果很多时候比瞎猜还不如,所以如果你已经知道数据之间的联系是非线性的,千万不要迷信逻辑回归)
- 逻辑回归计算快:对于线性数据,逻辑回归的拟合和计算都非常快。
- 逻辑回归返回的分类结果不是固定的0,1,而是以小数形式呈现的类概率数字:我们因此可以把逻辑回归返回的结果当成连续型数据来利用。 比如在评分卡制作时,我们不仅需要判断客户是否会违约,还需要给出确定的”信用分“,而这个信用分的计算就需要使用类概率计算出的对数几率。
- 逻辑回归还有抗噪能力强,在小数据集上表现更好。
